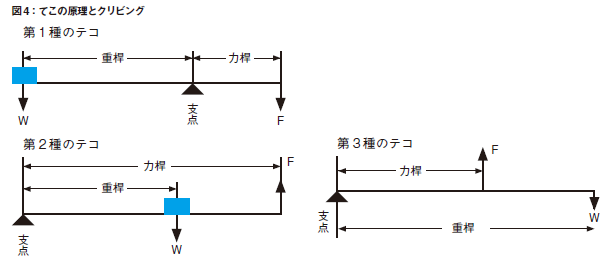
てこ比 データに外れ値があると、回帰式の推定値が大きく変わってしまう可能性がある。 重回帰分析での、推定偏回帰係数は次のように求められる。 予測値は次のようになる。 tak******** さん 09/8/2 1055 1 1 回答 第2種のテコの計算式を教えてください。 第2種のテコの計算式を教えてください。 重量Wの値はkgf そこから支点までは40cmで、支点から力点Fまでの距離は150cmです。 続きを読む 物理学 ・ 8,744 閲覧第6話 ソフトを使った勉強−てこ比の性質− (六一学者の千字一話) 少し進んだ回帰分析のテキストには,てこ比の定義やその性質が解説されている.例えば, てこ比は,回帰分析の観察点(サンプル)ごとに,説明変数のデータを変えずに目的変数yの

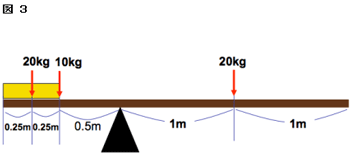
中3理科 仕事の原理 滑車 斜面 てこの仕事の計算 Pikuu
てこ 計算 中学
てこ 計算 中学-解き方 (クリックで表示) 支点からの距離×重さが、左右同じとき釣り合う 下向きの力=上向きの力 ↑これを覚えておけば解ける問題です。 バネばかりの重さを問う問題の場合、まず上向きの力と下向きの力を式で表します。 ? ×50cm 上向きの力 10g×50cm表→関係式2 文章→関係式 データとグラフ 比例反比例 (入試問題) → スg スム版は別包ソス スy ス ス スz ストゑソス スフ鯉ソス ス ス ス@ ス ス スフ図 スフよう スネ「 ストゑソス スv スノゑソス ス ス ストは, ス@ スi ス ス ス ス スフ重 ス ス スj ス




高校物理 力のモーメントの計算 映像授業のtry It トライイット
が測量計算の基本である。 ・三角法による計算 三角法とは、三角形を構成する角度や辺の長さの相対的な法則を利用して、長さや 角度などの位置関係を求めるものであり、三角関数や三平方の定理などに代表される。 図-6に三角法による計算例を示す。テコム模試のポイント 模試ラインナップ 問題数 計算問題、5肢択一、5肢択二問題、写真などのカラー視覚素材を使った問題の他に、長い状況文を付した単問の状況設定問題も含んでいます。自転車には、てこがいっぱい使われています。 まず、車輪の向きを変えるハンドル。 力点が支点から遠いところにあるので小さな力で、向きを変えることができるのです。 自転車を止めるブレーキ。 ここが支点。 力点、作用点です。 車輪を回すとき
基礎シリーズ第5弾。てこの原理で地球も動かせる?倍力機構の概要&てこ、トグル、クランク機構を用いた使用事例をご紹介 倍力機構とは / てこ機構 トグル機構 倍力機構の使用例 今月の特集では、倍力機構の定義、倍力機構に使われている機構と例を分アクスル負荷計算 アクスル荷重計算の概要 0401 発行 1 jaJP 4 (19) テコの原理 テコの原理は以下の例で説明できます(例中の手押し車は無重量と仮定されま す)。 手押し車の2個の地上の支点は片端の車輪と他端を持ち上げる人とから成り立っ ています。うにテコのたわみを光の反射角の変化として検出する方法 が多く採用されていますこ のような光の反射角の変化を 検出する方法を光テコ方式と呼びます光 テコの先端に付 いた突起によって被検面上を走査し,光 テコの上面のミ
ら次式で計算できます4,5. σ max = M max Z (56) したがって,最大曲げ応力を計算するためには,曲げ応力の分布と断面係 数を求めなくてはなりません.また,断面係数は次式で求められます. Z = I y max (57) ここで,Im4は図形の断面二次モーメント,yTitle urapdf Created Date AM基礎シリーズ第5弾。てこの原理で地球も動かせる?倍力機構の概要&てこ、トグル、クランク機構を用いた使用事例をご紹介 倍力機構とは / てこ機構 トグル機構 倍力機構の使用例 倍力機構② トグル機構 トグル機構は2つのリンクとスライダーから構



てこの原理に関連する計算を分かりやすく解説 具体例で学ぶ数学



てこのつり合い 力のつり合いとモーメントのつり合いが超便利 みみずく戦略室
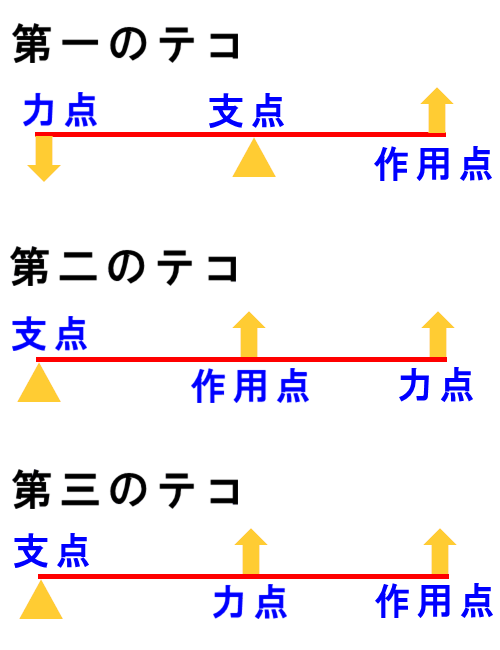
開リンク機構の一例 2 3 4 1 3自由度逆解析にあたる。実際の問題では逆解析のニーズの方が多いと思うが、計算上は複雑になり 一意の解が求まらない場合もある。 図4-7 マニピュレータのキネマティクス解析例 φ3 x1 x3 x2 φ2 φ1しらべてみよう NHK for Scool 第3種てこ 支点 、 力点 、 作用点 の3つの点を一直線上に並 (なら) べたとき、 力点 が間に位置する てこ 。 この



第7章 市民レベルの捜索 救助活動 後編 災害から命を守れ 市民 従業員のためのファーストレスポンダー教育 リスク対策 Com 新建新聞社



小学理科 てこのしくみ 学習ポスター クイズテスト やってみよう 無料ダウンロード ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習
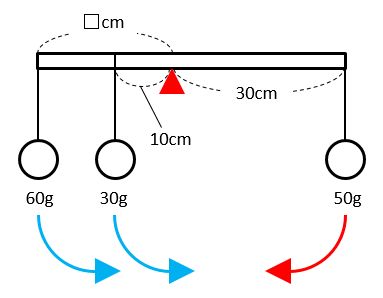
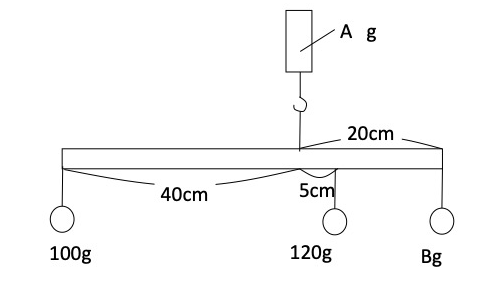
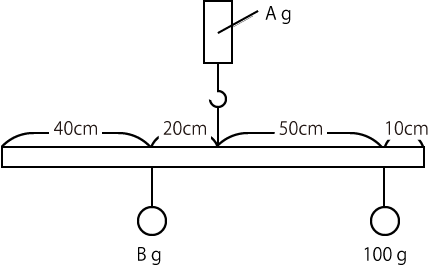
この場合は、 30 g(棒の重さ)+ 50 g (おもりAの重さ) + 100 g (右のおもりの重さ) = 180 g これが支点にかかる力です。 簡単ですよね。 単純に、 下向きにかかる力 と それを支える力 (つまり上向きにかかる力) は同じという事です。 だから棒やおもりが下にも落っこちず、上にふわふテコの原理を使えば、重い荷物を小さな力で動かすことができます。 この場合の支点に作用するモーメントは、m = f × lで計算すると誤りです。これは、計算の対象である作用力の領域で は、フランジは弾性域にあって、 降伏点 の違いの影響が出ないことを示している。しかし、大き目の作用力の場合には、フ ランジに降伏が生じ若干の相違が出る。そこでci としては算術平均を採用した。



てこの計算を得意になろう 1 辻義夫の中学受験に打ち勝つ家庭学習法




中学受験 文系ママさん必見 理科 てこ 4 はじめの一歩 定着までのチェックリスト 千葉のプロ家庭教師 大志 ブログ
点とするか、またその後の計算については、次の点に注意しましょう。 ① 計算がしやすくなるところを支点とする。 (解1)では、未知数であるばねはかりBを支点とすることで、Bの支点からの距離が 0㎝となります。リンクaを固定して、リンクbを回転 させると、リンクcを介して、リンクd は決まった動きをする。この連鎖 を1自由度の連鎖という(一つのリ ンクの動きが決まれば、ほかの動 きが決まる機構)。上腕二頭筋 ── 肘関節 設問2 運動の変数で正しいのはどれか。すべて選べ。 ワットは仕事率の単位である。 ニュートンは仕事の単位である。 仕事は力と移動距離の積で表す。 パワーは単位時間当たりの仕事である。 速度を時間で微分すると加速度




スイング探究 間違いだらけの テコの原理 ゴルフ I ステーション
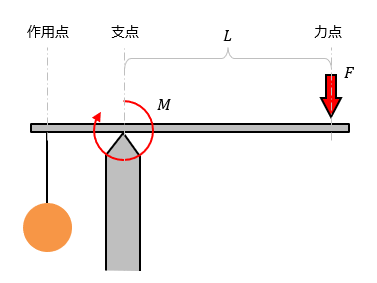



力のモーメント
5 力のモーメントは外積式で表され る M モーメントNm r モーメントアームm F 力N M = r ×F 力の作用線 r A 回転軸 H θ Fcosθ Fsinθ F O θ 力の垂直成分Fsinθによって回転が生じる Fsinθ最大:θ=90°のとき、モーメント最大 θ=0°,180°のとき、モーメントはゼロ→並進運動'dorized & Disinfected TECO (After) Deodorized & Disinfected C T 60 (Before) TECO (ppm) (min) =CTfifi (ppmxmin) CTfi (ppmxrnin) (ppm) (min) CTfi 60 ±30% (MRSA) TECO • IlLùñÄ 60 (At) s <回帰分析と分散分析に外れ値を特定する方法 モデル適合分析のコンテキストでは、外れ値は平均応答または予測変数の値よりも大きい観測値です。 Minitabには外れ値を識別するために複数の方法が用意されています。 これには、残差プロットおよび3つの




スイング探究 間違いだらけの テコの原理 ゴルフ I ステーション



1
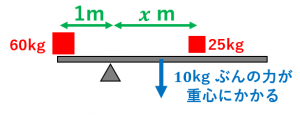
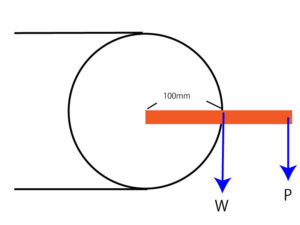
この状況のもとでテコの原理を使い、支点の左右で働く力を計算すればいいわけです。 まず左側の力として、金属版の重力による力075x=15と、テコ自身の重力による力 05x10=5 との合計で、とてこ比の計算は、次の方法で行います。 てこ比 (Lv) = 汎距離 (MH) / (データ 行数 - 1) + (1 / データ 行数 ) アドインプログラム販売価格: ¥3,000(税込) ※販売のみを行っております。 ご質問対応等のサポート及び改変は承っておりません AutoCADレギュラー版では寸法値の上書きを抽出する為のAutoLISPプログラムが公開されています。 それに比べれば少し手順が増えますが、AutoCAD LTの標準機能で寸法の上書きを探す方法を紹介します。 (1) 1辺が100mmの直線で作成された下図 (Fig1)のような図形




高校物理 力のモーメントの計算 映像授業のtry It トライイット



滑車と輪軸 りんじく はてこの原理 セルフ塾のブログ
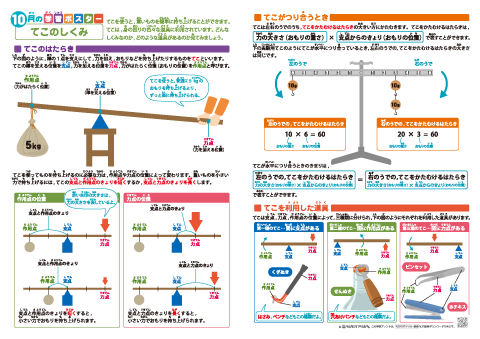
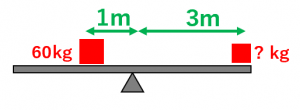
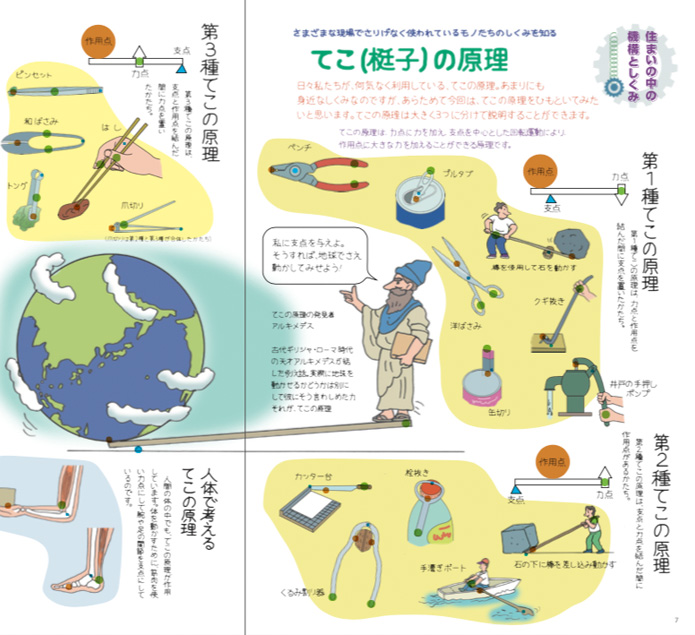
てこが水平になっているとき、左右の「てこをかたむけるはたらき」は同じ。 てこをかたむけるはたらきは、 「力の大きさ(おもりの重さ)×支点からのきょり(おもりの位置) で表すことができる。 力のつり合いや、てこの実験に使われる器具を小数点の計算が苦手な人は 「6×体重をして小数点を左へ2つずらす」 と考えてください。2桁×1桁の掛け算は小学3年生レベルの算数です。できるはずです。 体重50kgの人に3γ流すのは、1γ= 30mg/hだから3をかけて3γ= 90mg/h テコの原理で、パンタ式にするのはなぜですか? どのようなメリットがありますか? 小学生がわかるぐらい、詳しく&優しく教えてください。 / テコの原理と、パンタ式は、直接は関係がありません。 画像 写真の場合、テコの原理を使っているのは、油圧ジャッキの取り
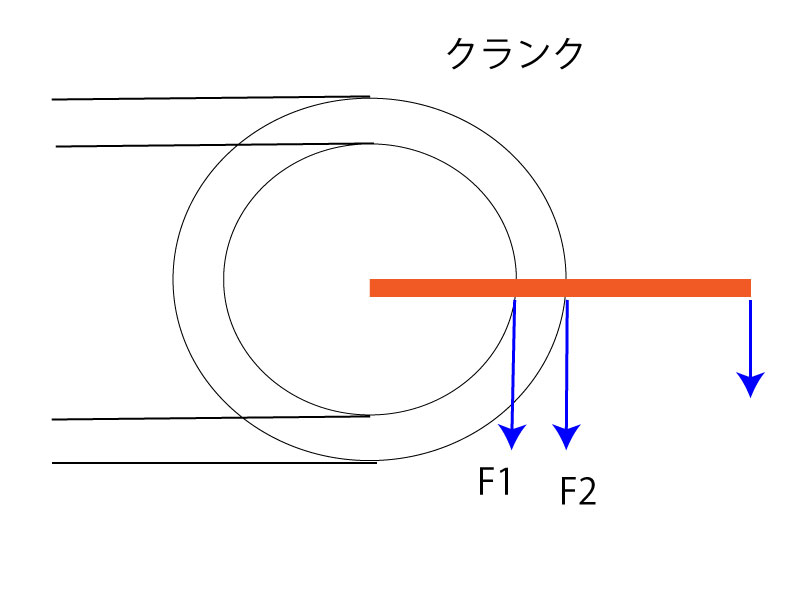



ギアの軽い 重いは テコの原理のほうが説明が早いかも




中学受験 文系ママさん必見 理科 てこ 4 はじめの一歩 定着までのチェックリスト 千葉のプロ家庭教師 大志 ブログ




中学受験理科講座 てこの性質




公立中高一貫校 適性検査でよく出る てこ てんびん 問題とは 恋する中高一貫校 適性検査 徹底攻略
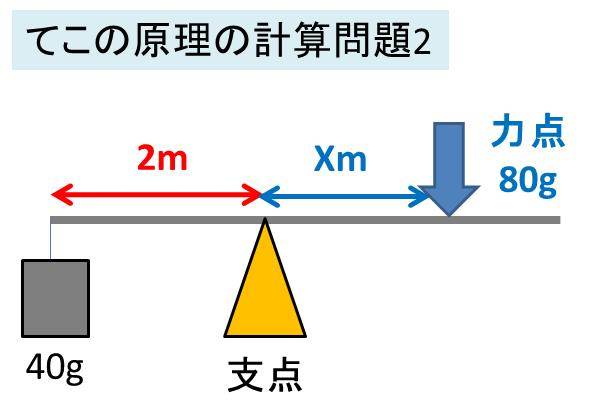



てこの原理を用いた計算方法 公式と問題




財務レバレッジとは Roeとの関係 計算式や目安を説明 Hupro Magazine




てこのつり合いの問題と解き方 支点を中心に左右のモーメントを計算する 小学理科 Irohabook



第3種のテコの計算式を教えてください 重量wの値は20kgfそこから支点ま Yahoo 知恵袋



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 さ ではじまるキーワード キーワード 作用点 て こ




大腿四頭筋とハムストリングスはてこの原理で動いています 痛くない人工膝関節手術2



イップス研究報告 夢工房ドリーム整骨院 イップス科学研究施設 神戸市灘区で結果にこだわった治療を行っています




中学受験理科講座 てこの性質




中学受験 文系ママさん必見 理科 てこ 4 はじめの一歩 定着までのチェックリスト 千葉のプロ家庭教師 大志 ブログ




てこの原理 公式を使った距離の計算と応用 力のモーメントのつり合い ささいな情報




財務レバレッジとは 計算式から経営の収益性を読み解く ビジドラ 起業家の経営をサポート




理基礎小学生理科 てこ 天秤 バネがわかる方法



Fiqx1l37ge5k4ncxx0j Net 03 08 Post 940



1
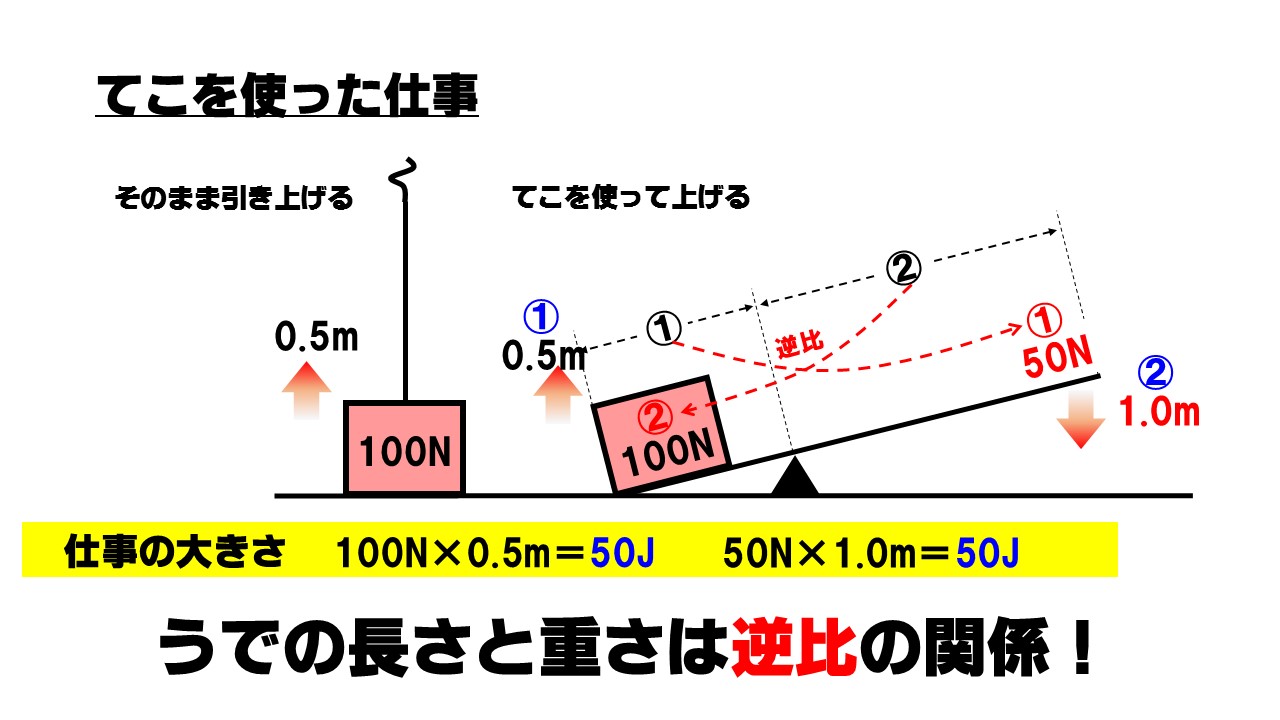



中3理科 仕事の原理 滑車 斜面 てこなどの道具を使った仕事 Examee
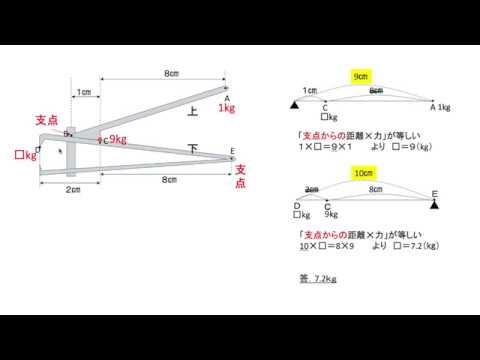



爪切り 身近な てこ Youtube



まっすぐでない棒を用いたテコの数値計算について 典型的な第三のテコ Yahoo 知恵袋
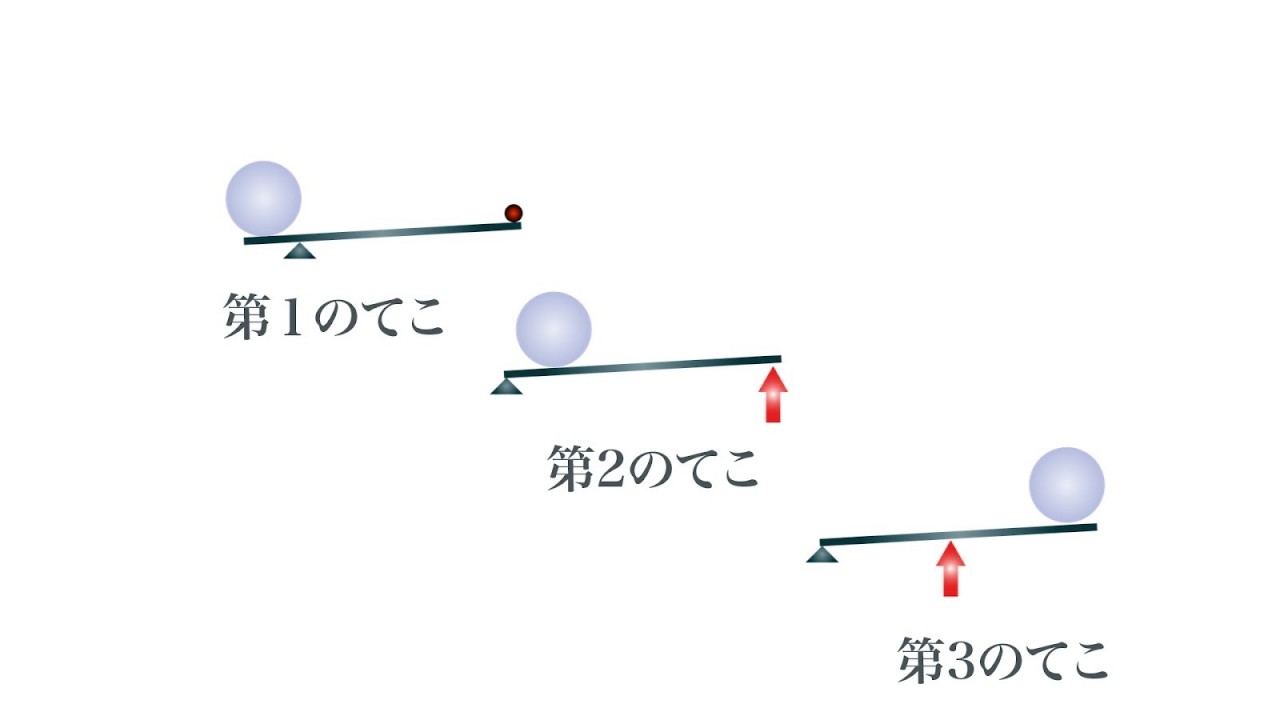



バールの使い方 イメージ
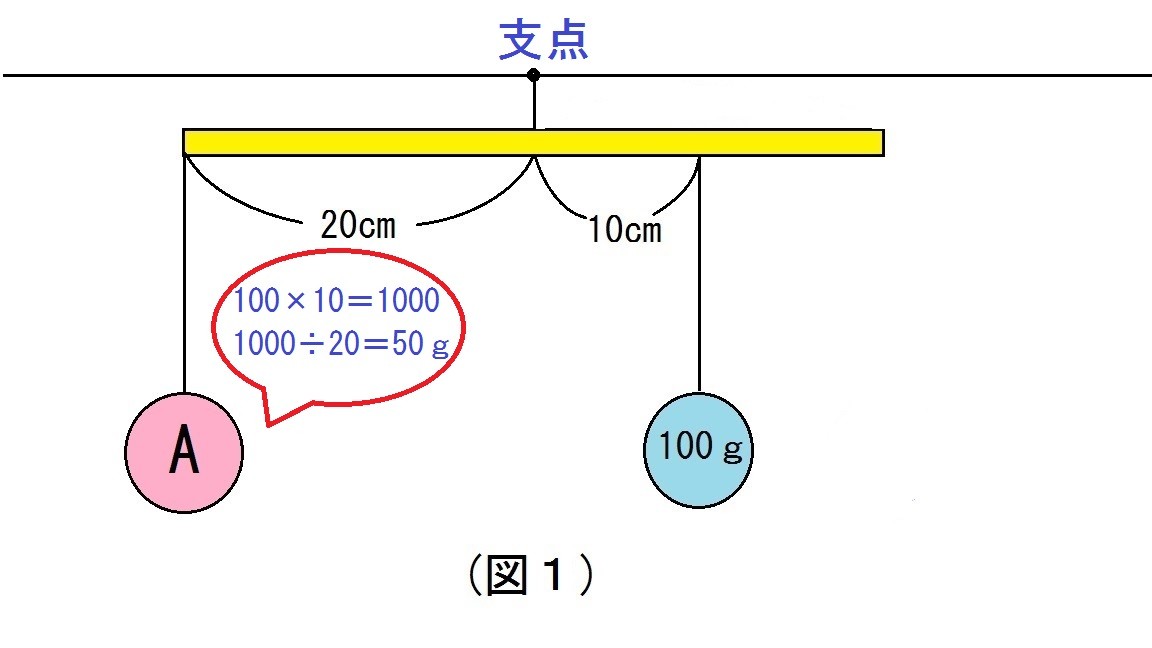



理科 本当に 分かる という事 てこその3 支点が支える力 エース学院



U9j6qrqkc3v Jp Rikigaku Html



3




てこのつり合いの問題と解き方 支点を中心に左右のモーメントを計算する 小学理科 Irohabook




力のつり合い てこ の問題の公式と解き方 中学受験 中学理科 Yattoke 小 中学生の学習サイト




てこの種類と人体での作用例 Study Channel



てこの原理の計算は 1分でわかる意味 計算と公式 距離 反比例 例題




レバレッジ効果とは はじめての不動産投資講座 みずほ不動産販売




ユーザーマニュアル
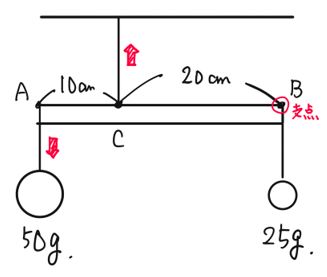



中学受験理科 てこ の対策 中学受験プロ講師ブログ



Science てこの問題を解くときに大切なこと 働きアリ
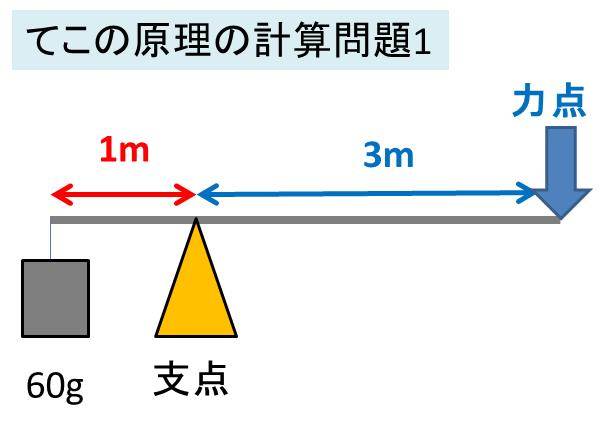



てこの原理を用いた計算方法 公式と問題



てこの原理に関連する計算を分かりやすく解説 具体例で学ぶ数学



2



てこの原理の解説 物理学解体新書



動画 中学受験 てこやばねの計算問題に強くなろう 1 勉強方法小学5年生の勉強法の中学受験情報メールマガジン 中学受験 個別指導のss 1 個別指導塾 オンライン個別指導



Science てこの問題を解くときに大切なこと 働きアリ




連載 その99 物理の基本的な考え方が大事
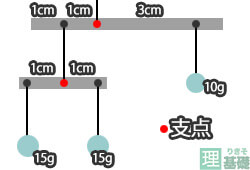



理基礎小学生理科 てこ 天秤 バネがわかる方法




板書ノート てこのはたらき




中3理科 仕事の原理 滑車 斜面 てこの仕事の計算 Pikuu




てこ 基本 Youtube



連載 その99 物理の基本的な考え方が大事




レバレッジ効果とは その意味や計算式をわかりやすく解説 資産運用 All About
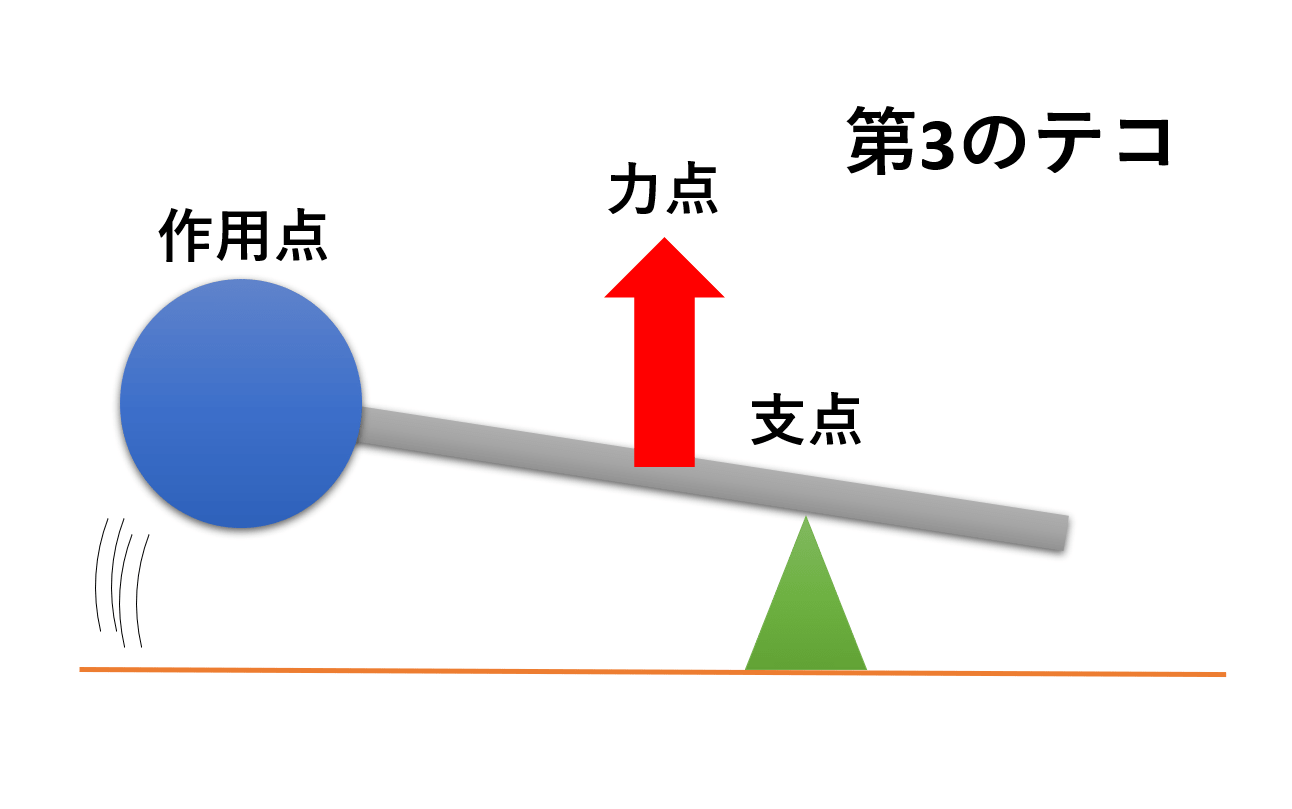



3種のテコ 第1のテコ 第2のテコ 第3のテコの違いを説明 陸上競技の理論と実践 Sprint Conditioning



第2種のテコの計算式を教えてください 重量wの値は20kgfそこ Yahoo 知恵袋
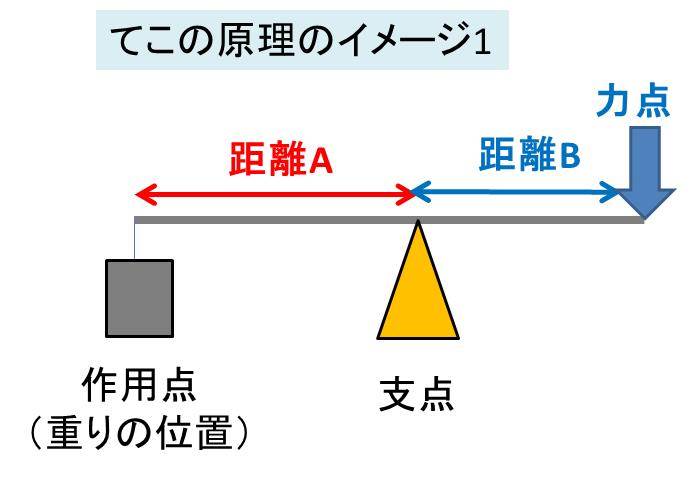



てこの原理を用いた計算方法 公式と問題
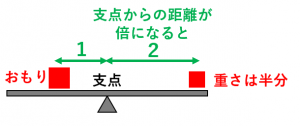



てこの原理に関連する計算を分かりやすく解説 具体例で学ぶ数学
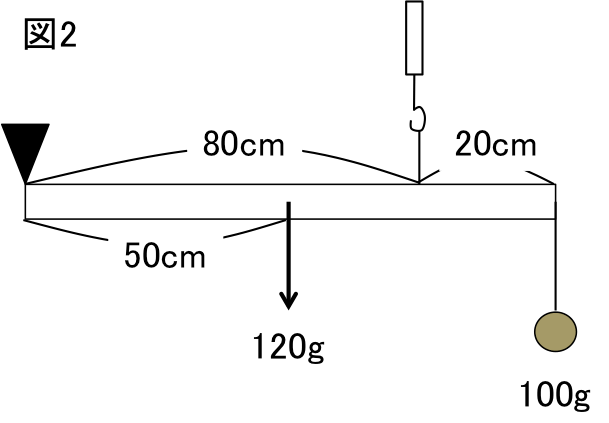



重さのあるてこをマスターしよう 辻義夫の中学受験に打ち勝つ家庭学習法



武井咲と柳田理科雄のラジオ空想科学研究所
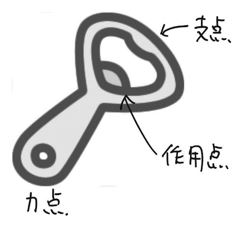



中学受験理科 てこ の対策 中学受験プロ講師ブログ



ボディメカニクスの基礎知識 テコとベクトル1 ボディメカニクスのお話
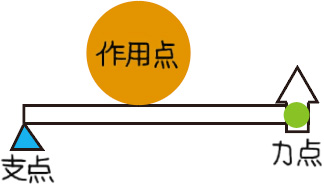



てこ 梃子 の原理 アトムcsタワー



Science てこの問題を解くときに大切なこと 働きアリ



ショートクランクとパワーの関係性 ショートクランク化で必要とされるパワーはどれくらい




支点の数で使い心地が変わる ーホチキスの性能を調査ー 生活科学研究室 エフシージー総合研究所




質問 は第2のテコですか の計算式と答えを教えてください Clear
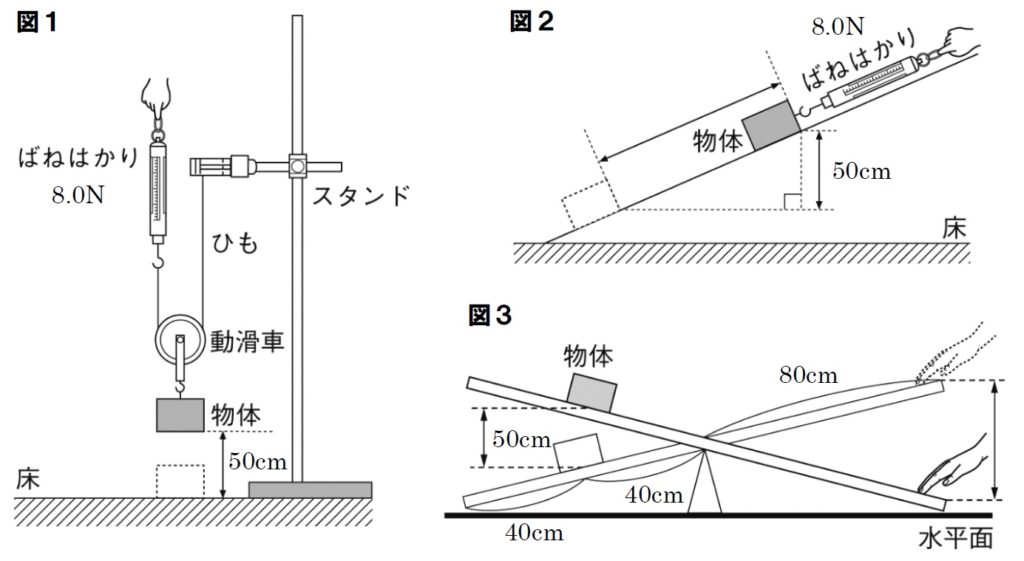



中3理科問題 仕事の原理 滑車 斜面てこの計算問題 Examee




蒸留の てこの原理 を解説 簡易的に気液平衡を計算 化学工学レビュワー




てこの計算を得意になろう 1 Youtube




てこが水平につりあう時のきまり 家庭学習レシピ
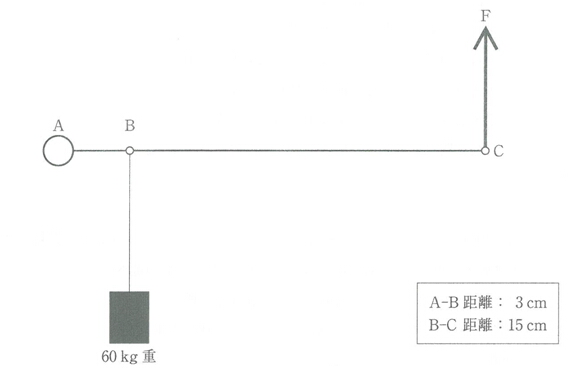



解説 第50回理学療法士国家試験問題 50p19 計算問題 てこ トレンドの樹



Http Www Tm Hum Titech Ac Jp Basic Biomechanics 6 Pdf
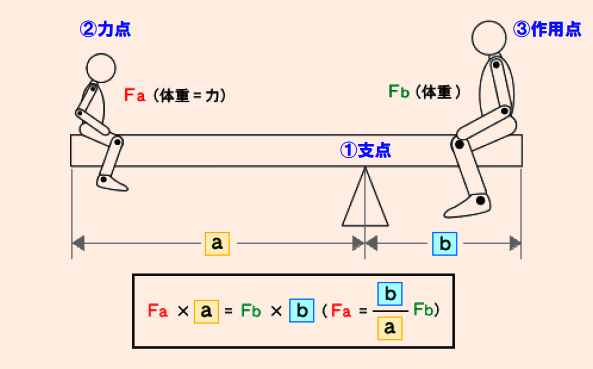



倍力機構とは てこ機構 倍力機構の基礎 技術情報 Misumi Vona ミスミ



てこ 梃子 の原理 アトムcsタワー




てこ 本当に支点はどこでもいいの Youtube
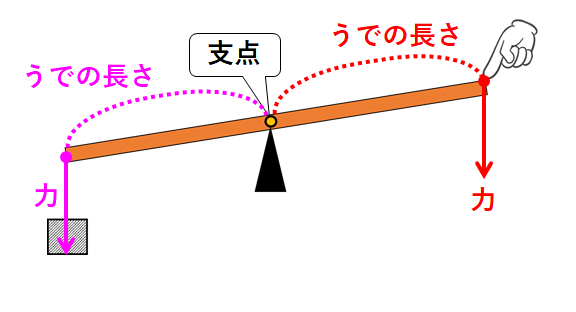



中3物理 てこをつかった仕事 中学理科 ポイントまとめと整理




てこが水平につりあう時のきまり 家庭学習レシピ



てこの原理と計算




公立中高一貫校 適性検査でよく出る てこ てんびん 問題とは 恋する中高一貫校 適性検査 徹底攻略



1
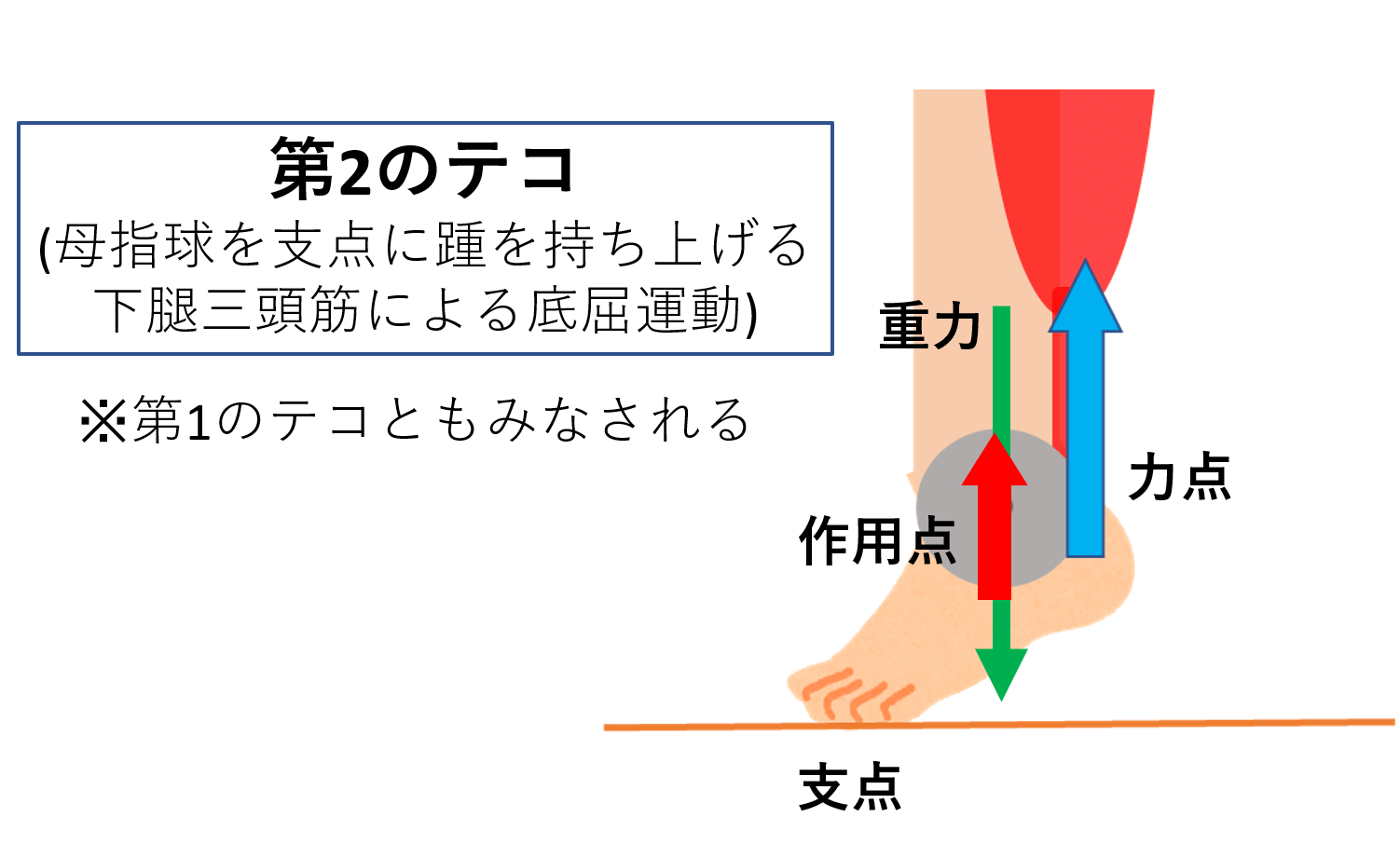



3種のテコ 第1のテコ 第2のテコ 第3のテコの違いを説明 陸上競技の理論と実践 Sprint Conditioning



第3種のテコの計算式を教えてください 重量wの値は20kgfそこから支点ま Yahoo 知恵袋




理科 本当に 分かる という事 てこその3 支点が支える力 エース学院
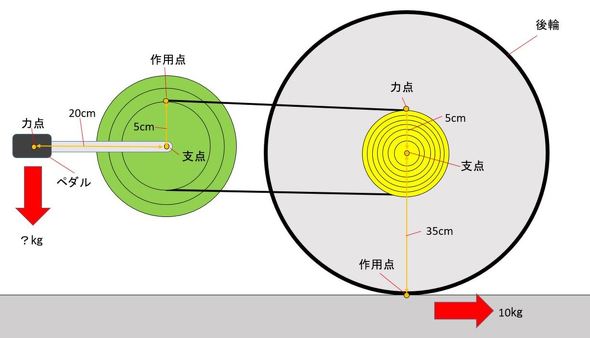



自転車のタイヤを回す 巻き掛け伝動機構 とギアチェンジの仕組み 身近なモノから学ぶ機構設計 超 入門 8 2 3 ページ Monoist



連載 その99 物理の基本的な考え方が大事



Science てこの問題を解くときに大切なこと 働きアリ



一般社団法人日本クレーン協会




独り言 ストロークとトルクとテコの原理 Boogiemenのブログ 南の国が大好きです みんカラ



関節モーメントとは 義肢装具士のための基礎力学




てこの原理 の計算方法 垂直方向に10kgf 力点 の力がかかり 真左 物理学 教えて Goo



第3種のテコの原理 Regnirt Sorpの日記




てこ 支点が端 Youtube
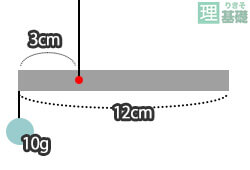



理基礎小学生理科 てこ 天秤 バネがわかる方法
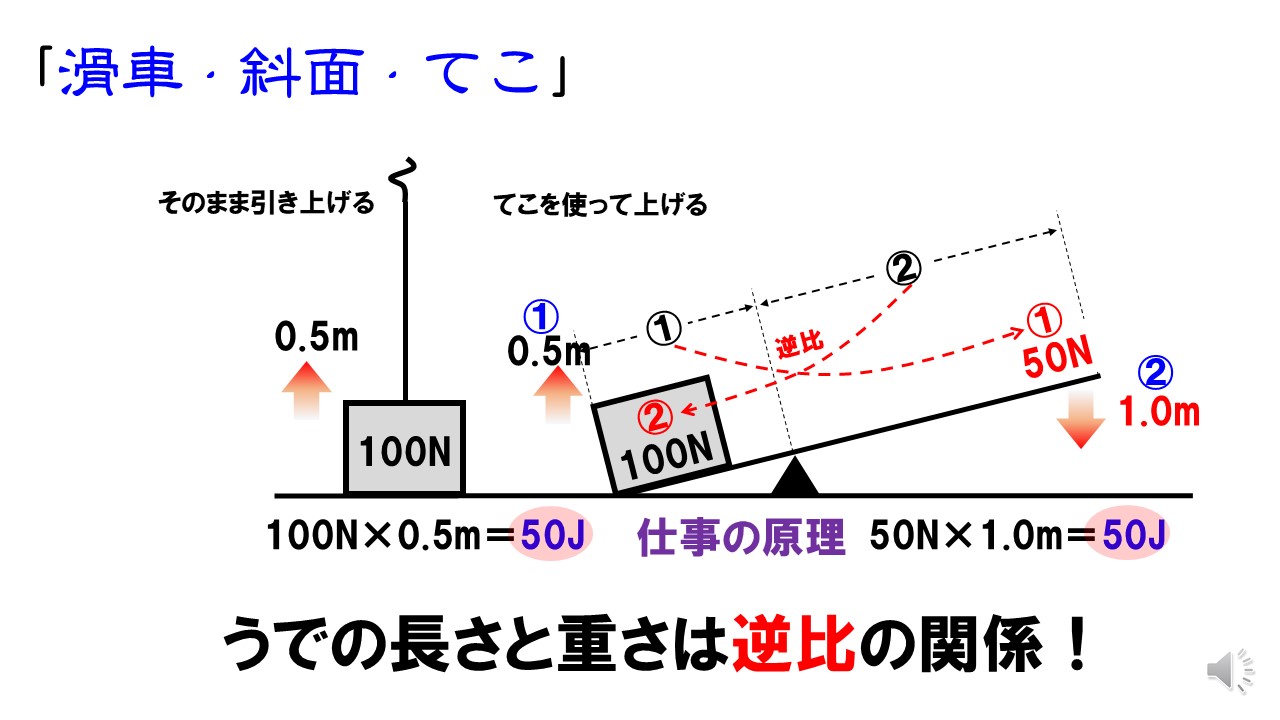



中3理科 仕事の原理 滑車 斜面 てこの仕事の計算 Pikuu



Http Www Tm Hum Titech Ac Jp Basic Biomechanics 6 Pdf



力のモーメントってなに 本当にわかるモーメントの意味と計算方法



てこの原理の計算は 1分でわかる意味 計算と公式 距離 反比例 例題




てこの原理 の計算方法 垂直方向に10kgf 力点 の力がかかり 真左 物理学 教えて Goo




てこの原理の計算方法 てこの原理についての質問です 45度に傾いた 数学 教えて Goo



0 件のコメント:
コメントを投稿